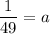Question

The vertex of this parabola is at (-3, -1). When the y-value is 0, the x-value is 4. What is the coefficient of the squared expression in the parabola's equation?

Answer 1

S(-3, -1)

P(4, 0)

a = (Py - Sy) / (Px - Sx)^2

a = (0 - (-1)) / (4 - (-3))^2

a = 1 / 7^2

a = 1 / 49

Answer 2

Answer:
`\bold{(1)/(49)}`

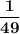
Explanation:

The vertex form of a quadratic equation is: y = a(x - h)² + k where

• "a" is the coefficient
• (h, k) is the vertex

Since the given information is (h, k) = (-3, -1) and (x, y) = (4, 0), we can input those values into the vertex form and solve for "a":

0 = a[4 - (-3)]² + (-1)

0 = a(4 + 3)² - 1

0 = a(49) - 1

1 = 49a

`(1)/(49)=a`