Answer:
3
Explanation:
The boxes are stacked 5 boxes deep by 4 boxes high by 4 boxes across, then there are
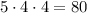 boxes in total.
boxes in total.
The mass of 1 box of paper is 22.5 kilograms, so 80 boxes weigh
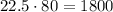 kilograms.
kilograms.
When the driver is in the truck, the mass is 2948.35 kilograms, then the total mass is
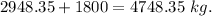
Let n be the number of boxes of paper the driver must deliver at the first stop. Their weigth is 22.5n kg and the weight of the truck without n boxes is
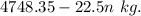
Trucks with a mass greater than 4700 kilograms are not allowed over the bridge, thus
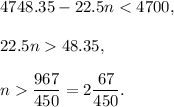
Hence, the driver must deliver at least 3 boxes at the first shop.