Answer:
shorter side: 5 km
longer side: 27 km
Explanation:
So you're already given the formula for the area of a rectangle, the next thing to do is assign length and width in terms of some unknown variable, which for convenience, I'll just say is x. So let's say one of the sides is x, the one that's the shorter side, since the longer side can be related to the shorted side, which is x. The longer side is 12km longer than 3 times the other side, so since the other side is x, it's length is (3x+12). So we simply multiply this by x, to get the area which is 135
"Known" Values: one side=x, other side=3x+12, area=135 km^2
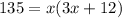
Distribute the x

Subtract 135 from both sides
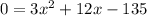
Now since the equation is equal to zero, we can use the quadratic equation. In this case a=3, b=12, and c=-135
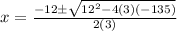
Simplify denominator and multiply inside of the radical
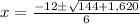
If you're confused where the negative went in the radical, it canceled out when multiply -4 by -135. Now add the stuff in the radical
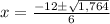
Simplify the radical
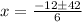
Now you might think there are two solutions to this equation, but the thing is that one of the sides simply cannot have a "negative length", because in this context, x must be positive. So it's easy to see you have to use the positive sign, since using the negative sign would result in -12-42 over 6 which is certainly negative. So we can ignore that solution as it doesn't mean anything in this context. We only need the positive solution
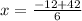
Add values

Divide
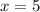
Since the shorter side was 5, that's the solution to the shorter side, now to find the longer side we plug in 5 into the equation:
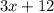 which becomes 3(5) + 12 = 15+12 = 27. This means the two lengths are 5 and 27
which becomes 3(5) + 12 = 15+12 = 27. This means the two lengths are 5 and 27