Answer:
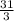
Explanation:
the formula for sums of geometric sequence (pls don't use what the other person said, it worked this time with the correct answer but it won't with others - that was just a coincidence!)
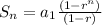
a1 = 1/3 since that's the first term
r = you divide the second term by the first term so 2/3 divided by 1/3 which is 2
n = the total number of numbers in the geometric sequence we're currently given so if you count there's 5
plug it all in and solve like normal fractions!
and you get 31/3