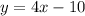1)The equation of the line in slope intercept form is

where

Blaine got this right.
Let
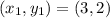
and
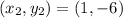
.
We find the slope by substituting the values into the slope formula;
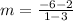
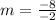

Blaine made a mistake here. He substituted the x-values for the y-values and vice-versa.
2) His new slope is 4.
To find the y-intercept, we substitute the slope and the point (1,-6) into the formula
This gives;
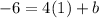
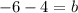
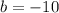
3) We now substitute the slope m=4 and y-intercept b=-10
The correct equation Blaine should have come up with is