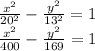Question

A hyperbola has its center at (0,0), a vertex of (20,0 and an asymptote of y= 13/20x. find the equation that describes the hyberbola

Answer 1

`(x^2)/(20^2) -(y^2)/(13^2) =1`

Explanation:

Given that a hyperbola has its centre at (0,0)

Asymptote = y =13x/20

Vertex is on x axis thus a =20

Hence hyperbola will have equation as

`(x^2)/(20^2) -(y^2)/(b^2) =1`

Asymptotes would be

`(x^2)/(20^2) -(y^2)/(b^2) =0`

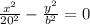
Or y=bx/20

Comparing with given equation we get b =13

Hence asymptote would have equation as

`(x^2)/(20^2) -(y^2)/(13^2) =1\\(x^2)/(400) -(y^2)/(169) =1`