Question

Trapezoids and kites

Answer 1

QUESTION 3

The sum of the interior angles of a kite is
`360\degree`.

`\Rightarrow 36\degree +70\degree+m<\:D+m<\:B=360\degree`.

`\Rightarrow 106\degree+m<\:D+m<\:B=360\degree`.

`\Rightarrow m<\:D+m<\:B=360\degree-106\degree`.

`\Rightarrow m<\:D+m<\:B=254\degree`.

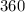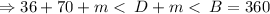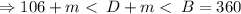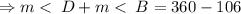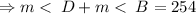But the two remaining opposite angles of the kite are congruent.

`\Rightarrow m<\:D=m<\:B`

`\Rightarrow m<\:D+m<\:D=254\degree`.

`\Rightarrow 2m<\:D=254\degree`.

`\Rightarrow m<\:D=(254\degree)/(2)`.

`\Rightarrow m<\:D=127\degree`.

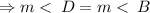
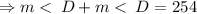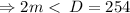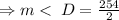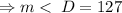QUESTION 4

RH is the hypotenuse of the right triangle formed by the triangle with side lengths, RH,12, and 20.

Using the Pythagoras Theorem, we obtain;

`|RH|^2=12^2+20^2`

`|RH|^2=144+400`

`|RH|^2=544`

`|RH|=√(544)`

`|RH|=4√(34)`

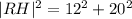
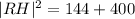
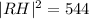
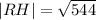
QUESTION 5

The given figure is an isosceles trapezium.

The base angles of an isosceles trapezium are equal.

Therefore
`m<\:T=60\degree`

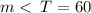
QUESTION 6

The measure of angle Y and Z are supplementary angles.

The two angles form a pair of co-interior angles of the trapezium.

This implies that;

`m<\:Y+68\degree=180\degree`

`\Rightarrow m<\:Y=180\degree-68\degree`

`\Rightarrow m<\:Y=112\degree`

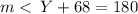
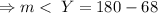
QUESTION 7

The sum of the interior angles of a kite is
`360\degree`.

`\Rightarrow 48\degree +110\degree+m<\:Q+m<\:S=360\degree`.

`\Rightarrow 158\degree+m<\:Q+m<\:S=360\degree`.

`\Rightarrow m<\:Q+m<\:S=360\degree-158\degree`.

`\Rightarrow m<\:Q+m<\:S=202\degree`.

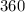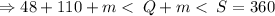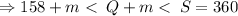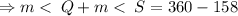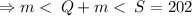But the two remaining opposite angles are congruent.

`\Rightarrow m<\:Q=m<\:S`

`\Rightarrow m<\:Q+m<\:Q=202\degree`.

`\Rightarrow 2m<\:Q=202\degree`.

`\Rightarrow m<\:Q=(202\degree)/(2)`.

`\Rightarrow m<\:Q=101\degree`.

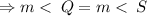
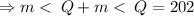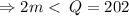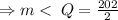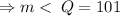QUESTION 8

The diagonals of the kite meet at right angles.

The length of BC can also be found using Pythagoras Theorem;

`|BC|^2=4^2+7^2`

`\Rightarrow |BC|^2=16+49`

`\Rightarrow |BC|^2=65`

`\Rightarrow |BC|=√(65)`

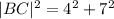
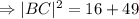
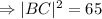
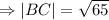
QUESTION 9.

The sum of the interior angles of a trapezium is
`360\degree`.

`\Rightarrow m<\:J+m<\:K+88\degree+120\degree=360\degree`.

`\Rightarrow m<\:J+m<\:K+208\degree=360\degree`.

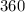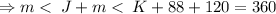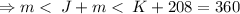But the measure of angle M and K are congruent.

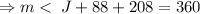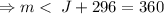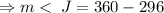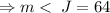`\Rightarrow m<\:J+88\degree+208\degree=360\degree`.

`\Rightarrow m<\:J+296\degree=360\degree`.

`\Rightarrow m<\:J=360\degree-296\degree`.

`\Rightarrow m<\:J=64\degree`.