Question

What is the solution of x+8/5x-1>0?

Answer 1

B

Explanation:

Edge2021

Answer 2

x<-8 or x>1/5

Explanation:

`(x+8)/(5x-1) >0`

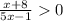
First we replace > symbol by = sign

`(x+8)/(5x-1) =0`

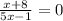
To solve for x we multiply 5x-1 on both sides

x+8 =0

x=-8

5x-1=0 solve for x

x= 1/5

WE got two values x=-8 and x= 1/5

Now we make a number line and check with each interval

x<-8, -8<x<1/5, x>1/5

Pick x= -9 and check with the given inequality

`(-9+8)/(5(-9)-1) >0`

1/46 >0 is true, so x<-8 satisfies our inequality

Pick x= 0 and check with the given inequality

`(0+8)/(5(0)-1) >0`

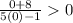
-8 >0 is false , -8<x<1/5 does not satifies our inequality

Pick x= 2 and check with the given inequality

`(2+8)/(5(2)-1) >0`

10/9>0 is true , x>1/5 satisfies our inequality