Question

Help with geometry hw

Answer 1

QUESTION 1

Let the third side of the right angle triangle with sides
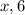`x,6` be
`l`.

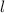Then, from the Pythagoras Theorem;

`l^2=x^2+6^2`

`l^2=x^2+36`

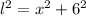
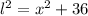
Let the hypotenuse of the right angle triangle with sides 2,6 be
`m`.

Then;

`m^2=6^2+2^2`

`m^2=36+4`

`m^2=40`

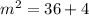
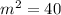
Using the bigger right angle triangle,

`(x+2)^2=m^2+l^2`

`\Rightarrow (x+2)^2=40+x^2+36`

`\Rightarrow x^2+2x+4=40+x^2+36`

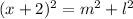
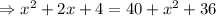
Group similar terms;

`x^2-x^2+2x=40+36-4`

`\Rightarrow 2x=72`

`\Rightarrow x=36`

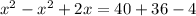
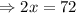
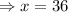
QUESTION 2

Let the hypotenuse of the triangle with sides (x+2),4 be
`k`.

Then,
`k^2=(x+2)^2+4^2`

`\Rightarrow k^2=(x+2)^2+16`

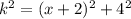
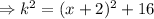
Let the hypotenuse of the right triangle with sides 2,4 be
`t`.

Then; we have
`t^2=2^2+4^2`

`t^2=4+16`

`t^2=20`

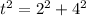
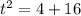
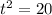
We apply the Pythagoras Theorem to the bigger right angle triangle to obtain;

`[(x+2)+2]^2=k^2+t^2`

`(x+4)^2=(x+2)^2+16+20`

`x^2+8x+16=x^2+4x+4+16+20`

`x^2-x^2+8x-4x=4+16+20-16`

`4x=24`

`x=6`

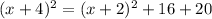
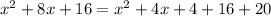
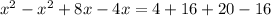
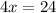
QUESTION 3

Let the hypotenuse of the triangle with sides (x+8),10 be
`p`.

Then,
`p^2=(x+8)^2+10^2`

`\Rightarrow p^2=(x+8)^2+100`

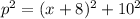
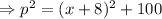
Let the hypotenuse of the right triangle with sides 5,10 be
`q`.

Then; we have
`q^2=5^2+10^2`

`q^2=25+100`

`q^2=125`

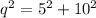
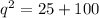
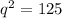
We apply the Pythagoras Theorem to the bigger right angle triangle to obtain;

`[(x+8)+5]^2=p^2+q^2`

`(x+13)^2=(x+8)^2+100+125`

`x^2+26x+169=x^2+16x+64+225`

`x^2-x^2+26x-16x=64+225-169`

`10x=120`

`x=12`

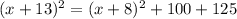
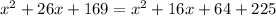
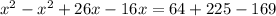
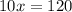
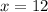
QUESTION 4

Let the height of the triangle be H;

Then
`H^2+4^2=8^2`

`H^2=8^2-4^2`

`H^2=64-16`

`H^2=48`

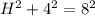
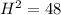
Let the hypotenuse of the triangle with sides H,x be r.

Then;

`r^2=H^2+x^2`

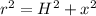
This implies that;

`r^2=48+x^2`

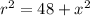
We apply Pythagoras Theorem to the bigger triangle to get;

`(4+x)^2=8^2+r^2`

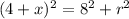
This implies that;

`(4+x)^2=8^2+x^2+48`

`x^2+8x+16=64+x^2+48`

`x^2-x^2+8x=64+48-16`

`8x=96`

`x=12`

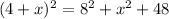
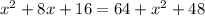
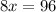
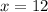
QUESTION 5

Let the height of this triangle be c.

Then;
`c^2+9^2=12^2`

`c^2+81=144`

`c^2=144-81`

`c^2=63`

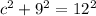
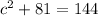
Let the hypotenuse of the right triangle with sides x,c be j.

Then;

`j^2=c^2+x^2`

`j^2=63+x^2`

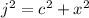
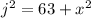
We apply Pythagoras Theorem to the bigger right triangle to obtain;

`(x+9)^2=j^2+12^2`

`(x+9)^2=63+x^2+12^2`

`x^2+18x+81=63+x^2+144`

`x^2-x^2+18x=63+144-81`

`18x=126`

`x=7`

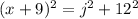
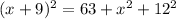
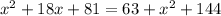
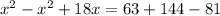
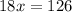
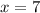
QUESTION 6

Let the height be g.

Then;

`g^2+3^2=x^2`

`g^2=x^2-9`

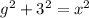
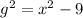
Let the hypotenuse of the triangle with sides g,24, be b.

Then

`b^2=24^2+g^2`

`b^2=24^2+x^2-9`

`b^2=576+x^2-9`

`b^2=x^2+567`

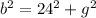
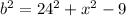
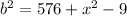
We apply Pythagaoras Theorem to the bigger right triangle to get;

`x^2+b^2=27^2`

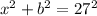
This implies that;

`x^2+x^2+567=27^2`

`x^2+x^2+567=729`

`x^2+x^2=729-567`

`2x^2=162`

`x^2=81`

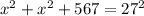
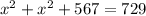
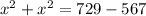
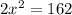
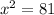
Take the positive square root of both sides.

`x=√(81)`

`x=9`

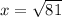
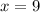
QUESTION 7

Let the hypotenuse of the smaller right triangle be; n.

Then;

`n^2=x^2+2^2`

`n^2=x^2+4`

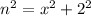
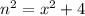
Let f be the hypotenuse of the right triangle with sides 2,(x+3), be f.

Then;

`f^2=2^2+(x+3)^2`

`f^2=4+(x+3)^2`

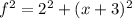
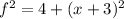
We apply Pythagoras Theorem to the bigger right triangle to get;

`(2x+3)^2=f^2+n^2`

`(2x+3)^2=4+(x+3)^2+x^2+4`

`4x^2+12x+9=4+x^2+6x+9+x^2+4`

`4x^2-2x^2+12x-6x=4+9+4-9`

`2x^2+6x-8=0`

`x^2+3x-4=0`

`(x-1)(x+4)=0`

`x=1,x=-4`

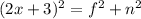
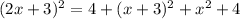
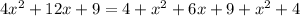
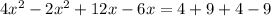
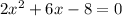
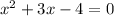
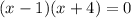
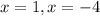
We are dealing with length.

`\therefore x=1`

QUESTION 8.

We apply the leg theorem to obtain;

`x(x+5)=6^2`

`x^2+5x=36`

`x^2+5x-36=0`

`(x+9)(x-4)=0`

`x=-9,x=4`

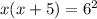
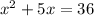
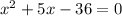
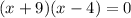
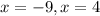
We discard the negative value;

`\therefore x=4`

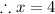
QUESTION 9;

We apply the leg theorem again;

`10^2=x(x+15)`

`100=x^2+15x`

`x^2+15x-100=0`

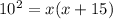
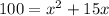
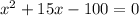
Factor;

`(x-5)(x+20)=0`

`x=5,x=-20`

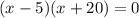
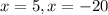
Discard the negative value;

`x=5`

QUESTION 10

According to the leg theorem;

The length of a leg of a right triangle is the geometric mean of the lengths of the hypotenuse and the portion of the hypotenuse adjacent to that leg.

We apply the leg theorem to get;

`8^2=16x`

`64=16x`

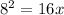
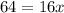
`x=4` units.

QUESTION 11

See attachment

Question 12

See attachment