Question

Which description compares the vertical asymptotes of function A and function B correctly?

Function A- f(x) = 1/x-1
Function B

A. Function A has a vertical asymptote at x =1
Function B has a vertical asymptote at x =0
B. Function A has a vertical asymptote at x = 1
Function B has a vertical asymptote at x = -3
C. Function A has a vertical asymptote at x = -1
Function B has a vertical asymptote at x= -3
D. Both functions have the same vertical asymptote.

Answer 1

Function A has a vertical asymptote at x = 1

Function B has a vertical asymptote at x = -3

Explanation:

Answer 2

Option B:

Function A has a vertical asymptote at x = 1

Function B has a vertical asymptote at x = -3

Explanation:

A function f(x) has a vertical asymptote if:

`\lim_(x \to\\k^+)f(x) = \±\infty\\\\ \lim_(x \to\\k^-)f(x) = \±\infty`

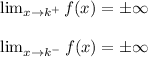
This means that if there is a value k for which f(x) has infinity or a -infinity then x = k is a vertical asymptote of f(x). Therefore, the closer x to k approaches, the closer the function becomes to infinity.

We can calculate the asymptote for function A.

`\lim_(x \to \\1^+)((1)/(x-1))\\\\ \lim_(x \to \\1^+)((1)/(1^-1))\\\\ \lim_(x \to \\1^+)((1)/(0)) = \infty\\\\and\\ \lim_(x \to \\1^-)((1)/(x-1))\\\\\lim_(x \to \\1^-)((1)/(0)) = -\infty`

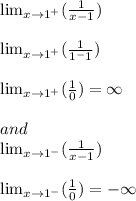
Then, function A has a vertical asymptote at x = 1.

The asymptote of function B can be easily observed in the graph. Note that the function b is not defined for x = -3 and when x is closest to -3, f(x) approaches infinity.

Therefore x = -3 is asintota of function B.

Therefore the correct answer is option B.