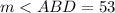Question

Properties of rectangle

Answer 1

4. y = 5

5. DB = 27

6. AC = 18

7. m<ABD = 53

Answer 2

For this case we have:

Question 1:

`BC = 24\\AD = 5y-1`

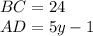
By definition, one of the properties of the rectangle states that:

The opposite sides of a rectangle have the same length, that is, they are equal, then:

`BC = AD`

So:

`24 = 5y-1`

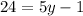
Clearing "y" we have:

`24 + 1 = 5y\\25 = 5y\\y = \frac {25} {5}\\y = 5`

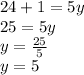
Thus, the value of "y" is 5.

Answer:

`y = 5`

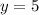
Question 2:

`AC = 2x + 13\\DB = 4x-1`

By definition, one of the properties of the rectangles states that:

The diagonals of a rectangle have the same lengths, that is:

`AC = DB\\2x + 13 = 4x-1`

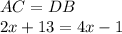
We clear the value of "x":

`13 + 1 = 4x-2x\\14 = 2x\\x = \frac {14} {2}\\x = 7`

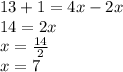
We must find DB:

`DB = 4x-1 \\DB = 4 (7) -1\\DB = 28-1\\DB = 27`

ANswer:

`DB = 27`

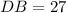
Question 3:

`AE = 3x + 3\\EC = 5x-15`

By definition, one of the properties of the rectangles states that:

The diagonals of a rectangle intersect and at the point of intersection they are divided in half, that is:

`AE = EC\\3x + 3 = 5x-15`

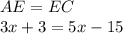
Clearing the value of "x" we have:

`3 + 15 = 5x-3x\\18 = 2x\\x = \frac {18} {2}\\x = 9`

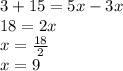
We know that:

`AC = AE + EC\\AC = 3x + 3 + 5x-15\\AC = 8x-12\\AC = 8 (9) -12\\AC = 60`

ANswer:

`AC = 60`

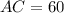
Question 4:

`m <ABD = 7x-31\\m <CDB = 4x + 5`

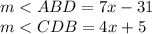
By definition, one of the properties of the rectangles states that:

The 4 angles of the rectangles are straight. From there it turns out that:

`m <ABD = m <CBD\\7x-31 = 4x + 5`

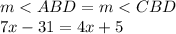
We clear the value of "x":

`7x-4x = 5 + 31\\3x = 36\\x = \frac {36} {3}\\x = 12`

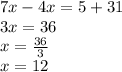
So:

`m <ABD = 7x-31\\m <ABD = 7 (12) -31\\m <ABD = 84-31\\m <ABD = 53`

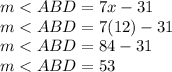
Answer:

`m <ABD = 53`