Question

Which answer represents the range of the logarithmic function given below?

F(x)=log0.5^x
A.) y is greater than or less than 0
B.) y<0
C.) y>0
D.) All real numbers

Answer 1

Option D is correct .i.e., All Real Number

Explanation:

Given Logarithmic Function,
`F(x)=log\,0.5^x`

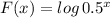
First we simply the function,

`F(x)=log\,0.5^x`

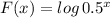
F(x) = x × log(0.5)

F(x) = -0.30103x (by putting value of log(0.5) )

Its clear range of F(x) completely depends on value of x .i.e, Domain of Function

Domain of log function is real Numbers

⇒ Ranges is also the Real Numbers

Therefore, Option D is correct .i.e., All Real Number

Answer 2

Answer: D) All real numbers

Explanation:

F(x) = log (0.5)ˣ

There is no restriction on x, so there is no restriction on y,

therefore y is all real numbers

see attached graph for verification