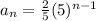Question

The recursive rule for a geometric sequence is given.

a1= 2/5; an= 5an−1

Enter the explicit rule for the sequence.

an=

Answer 1

`a_n= (2)/(5) (5)^(n-1)`

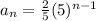
Explanation:

The recursive rule for a geometric sequence is given.

a1= 2/5; an=
`5a^(n-1)`

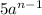
a1 is the first term = 2/5

USe the recirsive rule. compare an=
`ra^(n-1)`, where 'r' is the common ratio with the given recursive formula

r= 5, common ratio is 5

General explicit rule

`a_n= a_1(r)^(n-1)`

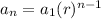
a1=2/5 and r= 5

So explicit rule becomes

`a_n= (2)/(5) (5)^(n-1)`

Answer 2

an = 2/5 * (5) ^ (n-1)

Explanation:

The common ratio is 5

(That is the number we multiply by)

The formula is

an = a1 (r) ^ (n-1)

an = 2/5 * (5) ^ (n-1)