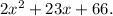Answer: The answer is
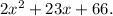
Step-by-step explanation: The given functions are
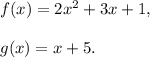
We are to find f(g(x)). To do this, first we need to evaluate g(x) and then we will apply the function f on the resulting function.
The evaluation is as follows:
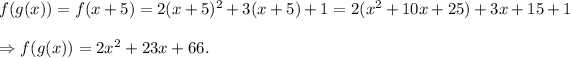
Thus, the correct answer is