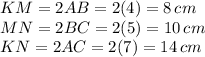Answer:
Explanation:
Two figures are said to be similar if their shapes are same but they differ in size .
We know that if two triangles are similar then their sides are proportional and angles are equal .
It's given that triangles ABC and KMN are similar .
In symbolic form ,
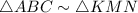
We need to find the lengths of the sides of the triangle .
We have
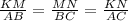
Given :
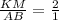
AB=4 cm, BC=5cm, CA=7 cm
Therefore,
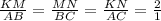
we get ,