Question

Two motorcyclists left point A for point B at the same time. The speed of one motorcyclist was 1.5 times greater than the speed of the other one. The motorcyclist, who reached point B first, immediately went back. He met the other motorcyclist in 2 hours and 24 minutes after the departure from point A. The distance between point A and point B is 120 mi. What is the speed of the cyclists and the distance from the point they met and point B?

Answer 1

40 mph, 60 mph, 24 miles

Explanation:

Let x mph be the speed of the slower motorcyclist, then 1.5x mph is the speed of the faster motorcyclist.

Both motorcyclists were travelling 2 hours 24 minutes = 2.4 hour. The slower motorcyclist drove
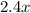`2.4x` miles and the faster motorcyclist drove
`2.4\cdot 1.5 x=3.6x` miles. In total, they both drove two distances from the point A to the point B, so

`2.4x+3.6x=2\cdot 120,\\ \\6x=240,\\ \\x=40\ mph,\\ \\1.5x=60\ mph.`

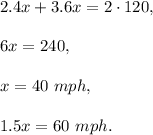
The slower motorcyclist drove

`2.4\cdot 40=96`

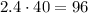
miles, so the distance from the point they met and point B is

`120-96=24`

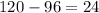
miles.