Question

The sum of two integers is -15. The product of the two integers is 54. What are those two integers a. -6 and -9 b. -6 and 9 c. 6 and 9

Answer 1

Let the two integers be x and y respectively

Hence;

`x + y = - 15 \\ \\ xy = 54`
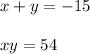
From the first equation ;

`x = - 15- y`
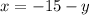
Substitute into the third equation

`( - 15 - y)y = 54`
Open up the bracket

`- 15y - {y}^(2) = 54`
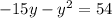
Take everything to the right hand side of the equation and you'll have a quadratic equation

`0 = 54 + 15y + {y}^(2)`
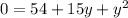
Solve the quadratic equation and you'll have two roots

`y= - 6 \: or \: y= -9`
Substitute for each value of y in the first equation
Therefore:

`x + ( - 6) = - 15 \: \\ or \\ \: x + ( - 9) = - 15`

`x - 6 = - 15 \\ or \\ x - 9 = - 15`

`x = - 15 + 6 \\ or \\ x = - 15 + 9`


`x = - 9 \: or \: x = - 6`
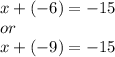
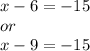
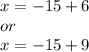
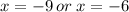
Therefore the answer is A