Question

The gravitational force between two objects is 3600N. What will be the gravitational force between the objects if the mass of each object is reduced to one-third of its original mass?

Answer 1

the answer is 400n

Step-by-step explanation:

I just took the quiz I hope you pass

Answer 2

400N:

`F = G(Mm)/(r^(2) )`

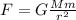
So lets make the first Force F1 and the second force after the reduction F2:

`F_(1) = G(Mm)/(r^(2) ) \\`

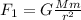
One third each mass so:

`F_(2) = G ((1)/(3)M (1)/(3) m )/(r^(2) )`

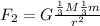
Pull out the constant:

`F_(2) = (1)/(9) (G(Mm)/(r^(2) ) )`

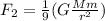
Now we can recognize that F1 equals all the stuff we have in parentheses so we can replace it!

`F_(2) = (1)/(9) F_(1)`

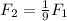
Now plug in our value for F1 which is 3600N

`F_(2) = (1)/(9) (3600)`

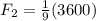
So:

F2 = 400N