Question

Use the identity (x+y)(x−y)=x2−y2 to find the difference of two numbers if the sum of the numbers is 12 and the difference of the squares of the numbers is 48.

Enter your answer as a number, like this: 42

Answer 1

The difference of two numbers is 7.

Explanation:

We have given that

The sum of the numbers is 12

x+y = 12

The difference of the squares of the numbers is 48.

x²-y² = 48

We have to find the difference of two numbers.

x-y = ?

Given formula is:

(x+y)(x-y) = x²-y²

Putting values in above formula, we have

(12)(x-y) = 48

x-y = 48 / 12

The difference of two numbers = x-y = 4 which is the answer.

Answer 2

The difference of two numbers using identity
`(x+y)(x-y)=x^2-y^2` is 4.

Explanation:

Given: The sum of the numbers is 12 and the difference of the squares of the numbers is 48.

To find the difference of two numbers using identity
`(x+y)(x-y)=x^2-y^2`

Let the two numbers be a and b, then

Given that the sum of the numbers is 12

that is a + b = 12 .........(1)

Also, given the difference of the squares of the numbers is 48.

that is
`a^2-b^2=48` ..........(2)

Using given identity
`(x+y)(x-y)=x^2-y^2`

We have
`(a+b)(a-b)=a^2-b^2`

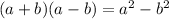
Substitute the known values, we have,

`12(a-b)=48`

Divide both side 12 , we have,

`(a-b)=4`

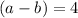
Thus, the difference of two numbers using identity
`(x+y)(x-y)=x^2-y^2` is 4.