Answer: Aproximately 2,525 balloons
Explanation:
1. Find the volume of a balloon with the formula given in the problem, where
 is the radius (
is the radius (
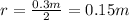 ), then:
), then:

2. Convert the volume from m³ to lliters by multiplying it by 1,000:
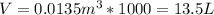
3. You know that that 1 liter of helium can lift 1 gram and that Ryan weighs 5 stone and 5 pounds. So you must make the following conversions:
1 g=0.0022 lb
From 5 stones to pounds

4. Then Ryan's weigh is:
5lb+70lb=75lb
5. Then, if 1 liter of helium can lift 0.0022 lb, to lift 75 lb (which is the weight of Ryan) they need:
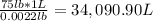
6. Then, to calculate the aproximated number of balloons they need to make him float (which can call
 ), you must divide the liters of helium needed to lift the weight of Ryan by the volume of a balloon, then the result is:
), you must divide the liters of helium needed to lift the weight of Ryan by the volume of a balloon, then the result is:
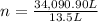
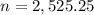 ≈2,525 balloons.
≈2,525 balloons.