Question

Solve for rational algebraic equation.

Answer 1

`x=2\\x=-(11)/(3)`

Explanation:

Solve the rational equation:

`\displaystyle (3x+4)/(5)-(2)/(x+3)=(8)/(5)`

To eliminate denominators, multiply by 5(x+3) (x cannot have a value of 3):

`\displaystyle 5(x+3)(3x+4)/(5)-5(x+3)(2)/(x+3)=5(x+3)(8)/(5)`

Operate and simplify:

`\displaystyle (x+3)(3x+4)-5(2)=(x+3)(8)`

`\displaystyle 3x^2+4x+9x+12-10=8x+24`

Rearranging:

`\displaystyle 3x^2+4x+9x+12-10-8x-24=0`

Simplifying:

`\displaystyle 3x^2+5x-22=0`

Rewrite:

`\displaystyle 3x^2-6x+11x-22=0`

Factoring:

`\displaystyle 3x(x-2)+11(x-2)=0`

`\displaystyle (x-2)(3x+11)=0`

Solving:

`x=2\\x=-(11)/(3)`

Answer 2

Explanation:

Taking the provided equation ,

`\implies (3x+4)/(5)-(2)/(x+3) =(8)/(5)`

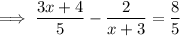
1) Here denominator of two fractions are 5 and x +3 . So their LCM will be 5(x+3)

`\implies ((x+3)(3x+4)-(2)(5))/(5(x+3))=(8)/(5)`

2) Transposing 5(x+3) to Right Hand Side . And 5 to Left Hand Side .

`\implies 5(3x^2+4x+9x+12 -10) = 40(x+3)`

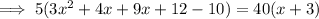
3) Multiplying the expressions.

`\implies 5(3x^2+13x+2) = 40x + 120`

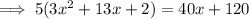
4) Opening the brackets .

`\implies 15x^2+ 65x + 10 = 40x + 120`

5) Transposing all terms to Left Hand Side .

`\implies 15x^2 + 65x - 40x + 10 - 120 = 0 \\\\\implies 15x^2 +25x - 110 = 0`

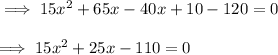
6) Solving the quadratic equation .

`\implies 5(3x^2+5x -22) = 0 \\\\\implies 3x^2+13x-22 = 0 \\\\ \implies x = (-b\pm √(b^2-4ac))/(4ac) \\\\\implies x = (-5\pm √(5^2-4(-22)(3)))/(2(3)) \\\\\implies x = (-5\pm √(289))/(6)\\\\\implies x =(-5\pm 17)/(6) \\\\\implies x = (17-5)/(6),(-17-5)/(6)\\\\\implies x = (12)/(6),(-22)/(6) \\\\\underline{\boxed{\red{\bf\implies x = 2 , (-11)/(3)}}}`