The fundamental theorem of algebra says this cubic has three roots, so we could write it as
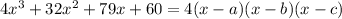
We're told one of the roots is equal to the sum of the other two, so we could take
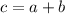 :
:

If we expand the right side, we get
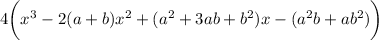
For two polynomial to be equal, the coefficients of terms of the same degree must match, so that
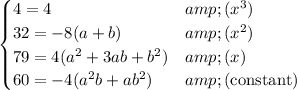
Now we can find
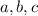 .
.
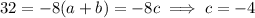
This tells us that
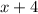 is a factor, so dividing the original cubic by this returns a remainder of 0.
is a factor, so dividing the original cubic by this returns a remainder of 0.

which further tells us that
 and
and
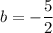 .
.