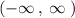Answer:
The domain for given function is
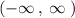
Explanation:
Given :
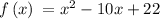
We have to find the domain of the given function.
Domain of a function is defined as a set of value for which the value of function is real and defined.
Consider the given function
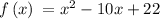
Since there is no points for x where the function f(x) is non defined.
Hence, whole number line is the domain for the given function.
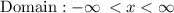
In interval form it is written as
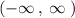
Thus, the domain for given function is