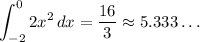Recall that the area of a trapezoid is equal to the average of its bases times its height.
For the trapezoids shown here, each base corresponds to the value of
 when
when
 is one of the endpoints of some interval, while the height is the length of that interval.
is one of the endpoints of some interval, while the height is the length of that interval.
On the interval [-2, -1], the trapezoids has bases 2(-2)² = 8 and 2(-1)² = 2, and "height" -1 - (-2) = 1. Then its area is (8 + 2)/2 × 1 = 5.
On the interval [-1, 0], one of the bases is 2(-1)² = 2 and the other is 2(0)² = 0, and the height is again 0 - (-1) = 1. Then the trapezoid's/triangle's area is (2 + 0)/2 × 1 = 1.
Then the total area under the curve
 on the interval [-2, 0] is approximately 5 + 1 = 6.
on the interval [-2, 0] is approximately 5 + 1 = 6.
Compare this to the actual value of the area given by the definite integral,