Answer:
Shown below
Step-by-step explanation:
A piecewise-defined function is a function defined by two or more equations over a specified domain. From the figure, our piecewise function is:

This function has been plotted below and we know some properties:
- The domain is the set of all real numbers
- The range is the set of all real numbers
- The function is the combination of two parabolas
- The point at which the these two parabolas meet is (0,0)
 is the parabola in purple while
is the parabola in purple while
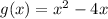 is the parabola in orange.
is the parabola in orange.