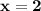Question

I)1-2(2x+1)=1-(x-1)
ii)3.6x-6.1=5.9_2.4x
question from equation and inequality​

Answer 1

1)Solving the expression
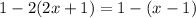`1-2(2x+1)=1-(x-1)` we get
`\mathbf{x=-(1)/(3)}`

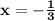
2) solving the equation
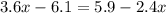`3.6x-6.1=5.9-2.4x` we get
`\mathbf{x=2}`

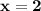
Explanation:

We need to solve the expressions:

1)
`1-2(2x+1)=1-(x-1)\\`

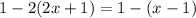
Solving

`1-2(2x+1)=1-(x-1)`

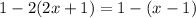
First solving the brackets

`1-4x-2=1-x+1`

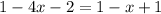
Simplifying

`-1-4x=-x`

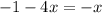
Adding 4x on both sides

`-1-4x+4x=-x+4x\\-1=3x`

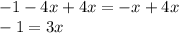
Switching the sides

`3x=-1`

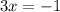
Divide both sides by 3

`(3x)/(3)=-(1)/(3)\\x= -(1)/(3)`

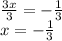
So, Solving the expression
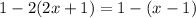`1-2(2x+1)=1-(x-1)` we get
`\mathbf{x=-(1)/(3)}`

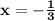
2)
`3.6x-6.1=5.9-2.4x`

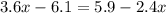
Solving:

`3.6x-6.1=5.9-2.4x`

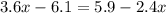
Adding 6.1 on both sides

`3.6x-6.1+6.1=5.9-2.4x+6.1\\3.6x=12-2.4x`

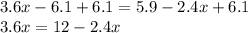
Adding 2.4x on both sides

`3.6x+2.4x=12-2.4x+2.4x\\6x=12\\`

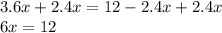
Divide both sides by 6

`(6x)/(6)=(12)/(6)\\x=2`

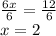
So, solving the equation
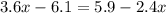`3.6x-6.1=5.9-2.4x` we get
`\mathbf{x=2}`