Question

What is the product of -2x^3 + x - 5 and x^3 - 3x - 4?

(A) Show your work

(B) is the prodyct of -2x^3 + x - 5 and x^3 - 3x - 4 equal to the product of x^3 - 3x - 4 and -2x^3 + x -5? Explain your answer.

Answer 1

a) Correct answer:

`boxed{-2x^6+7x^4+3x^3-3x^2+11x+20}`

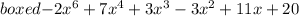
Step-by-step explanation:

To make the product of
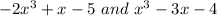`-2x^3+x-5 \ and \ x^3-3x-4`, we must group these two equations using parentheses as follows:

`(-2x^3+x-5)(x^3-3x-4) \\ \\ Then, \ let's \ apply \ distributive:\\ \\ (-2x^3)(x^3)+(-2x^3)(-3x)+(-2x^3)(-4)+(x)(x^3)+(x)(-3x)+(x)(-4) \ldots \\\ldots (-5)(x^3)+(-5)(-3x)+(-5)(-4) \\ \\ Solving: \\ \\ -2x^6+6x^4+8x^3+x^4-3x^2-4x-5x^3+15x+20 \\ \\ Grouping \ and \ solving: \\ \\\boxed{-2x^6+7x^4+3x^3-3x^2+11x+20}`

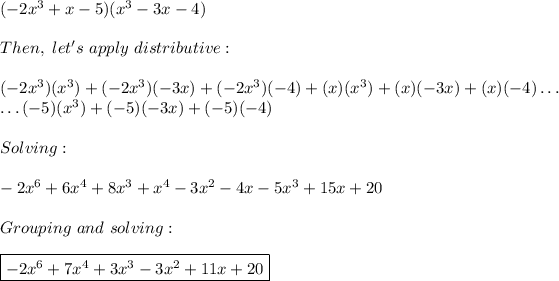
b) Correct answer:

They are equal

We have found the product of
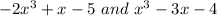`-2x^3+x-5 \ and \ x^3-3x-4` that is:

`(-2x^3+x-5)(x^3-3x-4)`

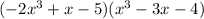
and whose result is:

`\boxed{-2x^6+7x^4+3x^3-3x^2+11x+20}`

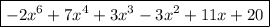
In this question, we need to find the product of
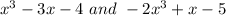`x^3-3x-4 \ and \ -2x^3+x-5` that is:

`(x^3-3x-4)(-2x^3+x-5)`

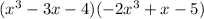
As you can see, this stands for the concept of commutative property that tells us that if you change the order of the operands, then the result doesn't change, that is, ab = ba. In conclusion:

`(-2x^3+x-5)(x^3-3x-4)=(x^3-3x-4)(-2x^3+x-5) \\ \\=-2x^6+7x^4+3x^3-3x^2+11x+20`