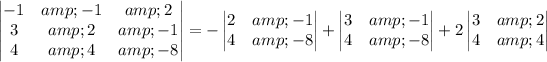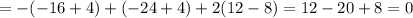The coefficient matrix is
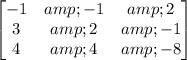
Notice that the last row is -4 times the first row, so that the rows of the matrix are not independent. This means the determinant would be 0.
Just to confirm, we can compute the determinant via a Laplace expansion along the first row: