Question

Type the correct answer in the box. Use numerals instead of words.

Adrian has a bag full of pebbles that all look about the same. He weighs some of the pebbles and finds that their weights are normally distributed, with a mean of 2.6 grams and a standard deviation of 0.4 grams.

What percentage of the pebbles weigh more than 2.1 grams? Round to the nearest whole percent.

Answer 1

89%

Explanation:

Answer 2

89% of pebbles weigh more than 2.1 grams.

Explanation:

Given that

Mean = 2.6

SD = 0.4

As we have to find the percentage of pebbles weighing more than 2.1, we have to find the z-score for 2.1 first

`z = (x-mean)/(SD)\\z = (2.1-2.6)/(0.4)\\z = -1.25`

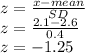
Now we have to use the z-score table to find the percentage of pebbles weighing less than 2.1

So,

`P(x<-1.25) = 0.10565`

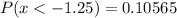
This gives us the probability of P(z<-1.25) or P(x<2.1)

To find the probability of pebbles weighing more than 2.1

`P(x>2.1) = 1 - P(x<2.1) = 1 - 0.10565 = 0.89435`

Converting into percentage

`0.89435*100 = 89.435\%`

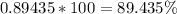
Rounding off to nearest percent

89%

Hence,

89% of pebbles weigh more than 2.1 grams.