Question

The actual distance between two villages is 120 kilometers. On a map of the area, 1 centimeter represents 3 kilometers.

What is the distance between the villages on the map?

Answer 1

40 cm.

Step-by-step explanation:

Let x be the distance between two villages on map.

We have been given that the actual distance between two villages is 120 kilometers. On a map of the area, 1 centimeter represents 3 kilometers.

We will use proportions to find the distance between villages on the map as proportion states that two fractions are equal.

`\frac{\text{Distance on map}}{\text{Actual distance}}=\frac{\text{1 cm}}{\text{3 km}}`

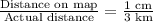
Upon substituting the actual distance between the two villages in our proportion we will get,

`\frac{x}{\text{120 km}}=\frac{\text{1 cm}}{\text{3 km}}`

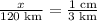
Let us multiply both sides of our equation by 120 km.

`\frac{x}{\text{120 km}}*\text{120 km}=\frac{\text{1 cm}}{\text{3 km}}*\text{120 km}`

`x=\frac{\text{1 cm}}{3}*120`

`x=\text{1 cm}*40`

`x=\text{40 cm}`

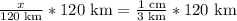
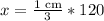
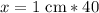
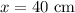
Therefore, the distance between two villages on the map is 40 cm.