Question

What is the quotient of d − 2 √ d 4 − 5 d 3 + d + 17

Answer 1

Answer:
`d^3 - 3d^2-5`

Explanation:

For finding the quotient of the given division,

In the long division method, we will follow the following steps.

Step 1 : Here the divisor is d-2 and dividend is
`d^4-5 d^3 + d + 17`

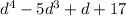
Multiply (d-2) by
`d^3` and subtract the dividend by the resultant.

We get
`-3d^3+d`

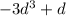
Step 2: Multiply (d-2) by
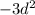`-3d^2` and subtract the remaining dividend by the resultant.

We get
`-5d^2+17`

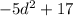
Step 3 : Multiply (d-2) by
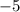`-5` and subtract the remaining dividend by the resultant.

We get
`7`

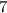
Since, after getting 7 it is not possible further division,

Hence, Remainder = 7,

Quotient = sum of all expression by that we multiply (d-2) =
`d^3 - 3d^2-5`