Question

The regular octagon ABCDEFGH rotates 135º clockwise about its center to form octagon A′B′C′D′E′F′G′H′. Point A′ of the image coincides with point of the preimage. Point B′ of the image coincides with point of the preimage.

Answer 1

Point A' will coincide D and B' will coincide with E.

Explanation:

In the figure attached we have regular octagon ABCDEFGH. It's a regular octagon means all it's sides are equal and central angle of one sector out of 8 sectors formed will be =
`(360)/(8)=45`

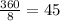
Now this octagon is rotated about it's center to form new octagon A'B'C'D'E'F'G'H'

Since angle of rotation is 135° clockwise which means octagon is rotated by 45×3 = 3×(central angle of one sector)

After rotation clockwise new image will coincide like this

A = F'

B = G'

C = H'

D = A'

E = B'

F = C'

G = D'

H = E'

Now we can easily tell that point A' will coincide with the point D of preimage. Similarly point B' of the image will coincide with the point E.

Answer 2

The point A′ of the image coincides with point D of the preimage. The point B′ of the image coincides with point E of the preimage.

Explanation:

It is given that regular octagon ABCDEFGH rotates 135º clockwise about its center to form octagon A′B′C′D′E′F′G′H′.

It means the central angle divided in 8 equal parts. The central angle between two consecutive vertices is

`(360)/(8)=45^(\circ)`

The regular octagon ABCDEFGH rotates 135º clockwise.

`A=F'`

`B=G'`

`C=H'`

`D=A'`

`E=B'`

`F=C'`

`G=D'`

`H=E'`

Therefore the point A′ of the image coincides with point D of the preimage. The point B′ of the image coincides with point E of the preimage.