Question

Find LCM of:

x2 - 9, 3x3 + 81​

Answer 1

`\boxed{\pink{\sf (x + 3) \ is\ the \ LCM . }}`

Explanation:

Given two expressions ,

`\qquad (1)\: x^2 - 9 \\\\ \qquad (2)\:3x^3 + 81`

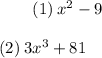
And , we need to find the LCM , that is lowest common factor . So , let's factorise them seperately .

Factorising x² - 9 :-

`= x^2 - 9 \\\\= x^2 - 3^2 \\\\ \red{= (x+3)(x-3)} \qquad\bf [Using \ a^2-b^2 = (a+b)(a-b) ]`

Factorising 3x³ + 81

`= 3x^3 + 81\\\\= 3(x^3+27) \\\\= 3( x^3+27) \\\\ = 3(x^3+3^3) \\\\ \red{= 3 [ (x+3)(x^2+9-3x) ] } \qquad \bf{[ Using \ a^3+b^3=(a+b)(a^2+b^2-ab) ] }`

Hence we can see that (x+3) is common factor in both expressions.

Hence the LCM is ( x+3 ) .