Any exterior angle is supplementary to any interior angle, so the sum of their measures is 180 degrees. If
 is the measure of one of these interior angles, then
is the measure of one of these interior angles, then
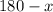 is the measure of the corresponding exterior angle.
is the measure of the corresponding exterior angle.
We're told that
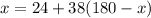
Solve for
 :
:
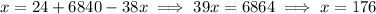
which means the exterior angles each have measure 180 - 176 = 4 degrees.
In a regular polygon with
 sides, the sum of the measures of all the exterior angles is 360 degrees:
sides, the sum of the measures of all the exterior angles is 360 degrees:
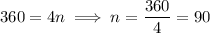
so this polygon has 90 sides.