Question

Suppose that 16 of the 80 state governors in a country were women. On each day of​ 2013, one of these state governors was randomly selected to read the invocation on a popular radio program. On approximately how many of those days should it be expected that a woman was​ chosen?

A woman was chosen on approximately
_____ of the days in 2013.

Answer 1

73 days.

Explanation:

The event that a female governor was chosen is independent between all days in 2013. The list of governors won't change so the chance will stay the same.

The question is asking for the number of successes in a fixed number of such independent trials. The Binomial Distribution will come handy for this purpose.

The Binomial Distribution asks for two parameters:

• The number of trials,
  `n`, and
• The probability of success on each trial,
  `p`.

Let success be that a female governor was chosen. There are 80 governors but only 16 are female.

`p = \frac{\text{Number of Qualified Choices}}{\text{Number of All Choices}} =(16)/(80) = (1)/(5)`.

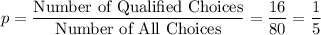How many days in 2013?

2013 is not a multiple of 4. The year 2013 is not a leap year. There are a total of 365 days in 2013.

Now, what's the expected value of a binomial distribution?

Given the distribution
`X` ∼
`B(n, p)`,

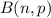• Expected value of
  `X`:
  `E(X) = n \cdot p`.

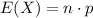Let
`X` be the number of days a female governor be chosen in 2013.

`X` ∼
`B(365, (1)/(5))`.

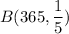Expected number of days a female governor be chosen in 2013:

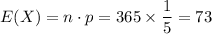`E(X) = n \cdot p = 365 * (1)/(5) = 73`.

Answer 2

Answer: 73

Explanation:

Create a proportion of governors to the total number of days in 2013

`(16)/(80)=(x)/(365)\\\\\\0.2 = (x)/(365)\quad \rightarrow \quad \text{simplified}\ (16)/(80)\\\\\\73=x\quad \rightarrow \quad \text{multiplied both sides by 365}`