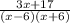Question

I need to be able to fully simply and state NPVs

Answer 1

see explanation

Explanation:

Factor the denominators of both fractions

x² - 36 = (x - 6)(x + 6) ← difference of squares

2x - 12 = 2(x - 6) ← take out common factor of 2

The sum can now be expressed as

`(x+5)/((x-6)(x+6))` +
`(4)/(2(x-6))`

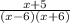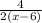
To make the denominators like

multiply the numerator/ denominator of the second fraction by (x + 6). At the same time cancelling the 2 and 4 on the numerator/ denominator

=
`(x+5)/((x-6)(x+6))` +
`(2(x+6))/((x-6)(x+6))`

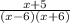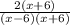
simplify the numerator by collecting like terms, leaving the denominator

=
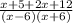
`(x+5+2x+12)/((x-6)(x+6))`

=
`(3x+17)/((x-6)(x+6))`