Question

Given f(x)=cos c and g(x)=cot x, what are the domain and range of f(g(x))?

Answer choices:

A. Domain: All real numbers; Range: all real numbers.

B. Domain: All real numbers x except x does not equal npi for all integers n; Range: all real numbers.

C. Domain: All real numbers x except x does not equal npi for all integers n; Range: -1 is less than or equal to y is less than or equal to 1.

D. Domain: All real numbers; Range: -1 is less than or equal to y is less than or equal to 1.

Answer 1

Option C

Explanation:

We know that the function
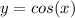`y = cos(x)` has as its domain all real numbers, and as a range
`-1\leq y\leq 1`

We know that the function
`cot(x) = (cos(x))/(sin(x))`

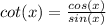
The denominator of the function can not be equal to 0. But
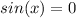`sin(x) = 0` for all
`x = n\pi` where n is an integer number.

Therefore the domain of cot(x) are all real numbers except
`x = n\pi`

The range of cot(x) are all real numbers

Then, the domain of f(g(x)) is:

x ∈ Domain g and g(x) ∈ Domain of f

Where:

Domain of g: All reals except
`x = n\pi`

Domain of f: All reals.

This is:

Domain of f(g(x)):

All real numbers except
`n\pi`

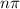
Range of f(g(x)):

`-1\leq y\leq 1`

Therefore the correct option is:

C. Domain: All real numbers x except x does not equal npi for all integers n; Range: -1 is less than or equal to and is less than or equal to 1.