Given is :
The radius of the spherical container = 13 units
A square plate rests horizontally in a spherical container and is 1 unit above the bottom point of the container. So, the distance from the center of the sphere to the center of the plate = 12 units. And the distance from the center of the sphere to the corner of the plate is 13 units.
Lets assume the side is 'x' units
Now using Pythagoras theorem, we will find the distance from the center of the plate to the corner :


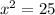
x=5 units
So, the length of the diagonal becomes 10 units.
Now, we get an isosceles triangle with sides x,x and 10 units.

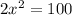
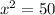
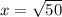
Hence, the length of a side of this plate is
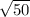 units.
units.