Question

Can someone please help me with these questions?

1) Identify the domain of the graph y= - 6x – 13
A) All real numbers
B) x <_ - 4
C) x >_ - 6
D) x >_ - 2

2) Determine which of the following statements is true concerning the values described in column #1 and column #2
Column 1: The x coordinate of the vertex of the graph of y= – 2x^2 – 4x + 12
Column 2: the x coordinate of the vertex of the graph of y = x^2 - 4x + 3
A) The value found in column #1 is greater then the value found in column #2
B) The value found in column #1 is less than the value found in column #2
C) The value found in column #1 is equivalent to the value found in column #2
D) The value found between column #1 and column #2 cannot be determined by the information given

3) A football is kicked toward the goal. The height of the ball is modeled by the function h(t)= —16t^2 + 64t where t equals the time in seconds and h(t) represents the height of the ball at time t seconds. What is the axis of symmetry and what does it represent?
A) t=2; it takes 2 seconds to reach maximum height and 2 seconds to fall back to the ground
B) t=2 ; it takes 2 seconds to reach maximum height and 4 seconds to fall back to the ground
C) t=4 it takes 4 seconds to reach maximum height and 4 seconds to fall back to the ground
D) it takes 4 seconds to reach maximum height and 8 seconds to fall back to the ground


4) choose the equation below whose axis of symmetry is x = 0

A) y= x^2 + 2x
B) y = x^2 – 16x + 58
C) y= x^2 + 2
D) y = x^2 – 4x + 2

Answer 1

QUESTION 1

The given function is


`y = - 6x - 13`

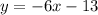
The domain of this function refers to all values of x for which y is defined.

The given function is defined for all real values of x.

The domain is all real numbers.

The correct answer is A

QUESTION 2

The equation in column 1 is


`y = - 2 {x}^(2) - 4x + 12`

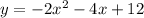
We obtain the vertex form as follows;


`y = - 2( {x}^(2) + 2x) + 12`


`y = - 2( {x}^(2) + 2x + {1}^(2)) - - 2 {(1)}^(2) + 12`


`y = - 2({(x + 1)}^(2)) + 2 + 12`


`y = - 2({x + 1)}^(2) + 14`

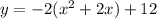
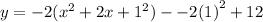
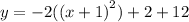
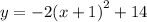
The x-value of the vertex is -1.

The equation in column 2 is


`y = {x}^(2) - 4x + 3`

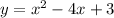
We can also find the x-value of the vertex using the formula,


`x = - (b)/(2a)`


`x = - ( - 4)/(2(1))`


`x = 2`
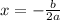
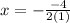
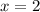
The correct answer is

B) The value found in column #1 is less than the value found in column #2

QUESTION 3

The height of the ball is modeled by


`h(t) = - 16 {t}^(2) + 64t`
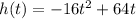
where t equals the time in seconds and h(t) represents the height of the ball at time t seconds.

The axis of symmetry can be found using the formula,


`t = - (b)/(2a)`


`t = - ( 64)/(2( - 16))`


`t = 2`

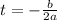
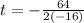
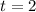
The correct answer is

A) t=2; it takes 2 seconds to reach maximum height and 2 seconds to fall back to the ground

QUESTION 4

The equation of axis of symmetry is given by the formula,


`x = - (b)/(2a)`

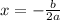
For the axis of symmetry of a given quadratic function to be zero, then the b-value of quadratic function should be zero.

The only equation from the given options whose b-value is zero is


`y = {x}^(2) + 2`

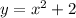
The axis of symmetry is


`x = - (0)/(2(1))`


`x = 0`

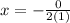
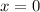
The correct answer is C