Answer:
After 64 minutes the tanks will have the same amount of water.
After 64 minutes the tanks will have 232 gallons of water
Explanation:
Part A.
We propose the equation for the first container. We call t the time in minutes that tank 1 takes to fill up and we call w the amount of water that tank 1 has as a function of time.
The tank starts with 8 gallons and every minute it fills 3.5 gallons more.
Then the equation is:
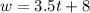
We propose the equation for the second container. We call t the time in minutes that tank 2 takes to fill and we call w the amount of water that tank 2 has as a function of time.
The tank starts with 24 gallons and every minute it fills 3.25 gallons more.
Then the equation is:
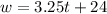
Part B
Now re.solvemos the system
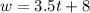 (i)
(i)
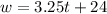 (ii)
(ii)
Now we introduce (i) in (ii)
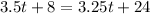
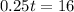
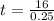
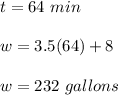
Part C.
After 64 minutes the tanks will have the same amount of water.
After 64 minutes the tanks will have 232 gallons of water