Question

An object is attached to a spring that is stretched and released. The equation d=-8cos(pi/6 t) models the distance, d, of the object in inches above or below the rest position as a function of time, t, in seconds. Approximately when will the object be 6 inches above the rest position? Round to the nearest hundredth, if necessary.

A)0 seconds
B)1.38 seconds
C)4.62 seconds
D)8 seconds

Answer 1

4.62

Explanation:

using the distance formula plug in the 6

6=-8cos(pi/6 t)

Answer 2

Option C - 4.62 seconds

Explanation:

Given : An object is attached to a spring that is stretched and released. The equation
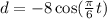`d=-8\cos((\pi)/(6) t)` models the distance, d, of the object in inches above or below the rest position as a function of time, t, in seconds.

To find : When will the object be 6 inches above the rest position?

Solution :

We have given the model,

`d=-8\cos((\pi)/(6) t)`

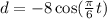
Where, d is the distance of the object in inches above or below the rest position and t is a function of time in seconds.

We have to find the time at which the object be 6 inches above the rest position i.e, for d=6.

Firstly we plot the graph of the given model,

Refer the attached graph below.

Now, the object be 6 inches above the rest position i.e, for d=6.

The time is t=4.62 seconds.

Therefore, Option C is correct.