Question

What is the explicit formula for the arithmetic sequence 4/5, 29/30, 17/15, 13/10?

Answer 1

B

Explanation:

E2020

Answer 2

Explicit formula is
`(4)/(5)+(n-1)((1)/(6))`

Explanation:

The given arithmetic sequence is 4/5, 29/30, 17/25, 13/10

The explicit formula of this sequence will be in the form of
`f{n}=A_(1)+d(n-1)`

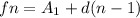
Where
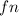`f{n}`= nth term of the sequence

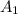`A_(1)`= first term of the sequence

n = number of terms

and d = Second term - first term

`d=(29)/(30)-(4)/(5) =(5)/(30) =(1)/(6)`

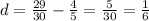
Now we put the values in the explicit formula

`f(n)=(4)/(5)+(n-1)((1)/(6))`

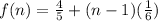
Therefore the explicit formula of this arithmetic sequence is f(n)=
`(4)/(5)+(n-1)((1)/(6))`