Answer:
Explanation:
The given equations are:
 (1)
(1)
and
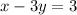 (2)
(2)
Now, simply adding equation (1) and equation (2), we get

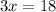

Now, substituting the value of x=6 in equation (2). we get


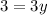
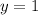
Thus, the values of x and y are 6 and 1 respectively.
In order to solve the system of solution, beau can see that in both the given equations, coefficient of y is same and is with opposite sign, thus simply adding both the equations will eliminate y and she will get the value of x and then substituting the value of x in any of the equations, she can get the value of y. With this, she can get closer to the solution.