Question

Choose the correct correspondence

Answer 1

Hello there

The right answer is S

:D

Answer 2

`\angle U \iff \angle S`

Explanation:

The graph shows to different figures. Assuming the internal triangles from each figure are congruent, then the corresponding element to
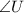`\angle U` is
`\angle S`.

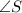Because, in the parallelogram UTSR, we have two triangles which are congruent. So, when we have a congruence between triangles, we deduct all corresponding elements that are congruent.

So, the congruence is between
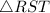`\triangle RST` and
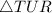`\triangle TUR`, from this congruence, we have

`\angle R \cong \angle T\\\angle S \cong \angle U\\\angle T \cong \angle R`

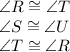
Therefore, the right answer is
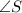`\angle S`.