Question

How many integers n satisfy both of the inequalities 4n + 3 < 25 and -7n + 5 < 24?

Answer 1

1) All real numbers n such that
`n < 5.5`

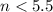
2) All real numbers n such that
`n > -(19)/(7)`

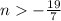
Step-by-step explanation: How did I come up with such answers? Let me show you!

For the first problem, we just solve the inequality easily.

Subtracting 3 from both sides, we get:

4n < 22

Dividing by 4 from both sides, we get:

n < 5.5

Thus, all real numbers n that is less than 5.5 when plugged in for x will be less than 25.

For the next problem, it will be slightly trickier.

Subtracting 5 from both sides, we get:

-7n < 19

Dividing -7 from both sides, we get:

n > -19/7

Did you catch that? We just flipped the inequality sign and turned it from less than to a greater than. Whenever we divide by a negative number, the signs always change.

Thus, for all real numbers n greater than -19/7, when plugging in for x, you will get less than 24.

Hope this helped!