Question

Country A and country B currently have the same population but the population of Country A is growing at a rate of 5% per year but the population of Country B is growing at a rate of 21.551% per year. What expression represents the ratio, when converted to a decimal, of Country A's population to Country B's population after x years? (1.05^4=1.21551)

Answer 1

Answer:
`f(x)= (0.863834933)^x`

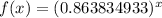
Explanation:

Let the initial population of country A represented by
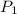`P_1` and the population of country B is represented by
`P_2`,

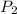Then, According to the question,

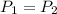`P_1=P_2` ----------(1)

Since, the population of country A is increasing at a rate of 5% per year,

Hence, the population of A after x years

`= P_1(1+0.05)^x`

`= P_1(1.05)^x`

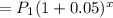
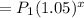
Similarly, the population of country B is increasing at a rate of 21.551 % per year,

Hence, the population of B after x years

`= P_2(1+0.21551)^x`

`= P_2(1.21551)^x`

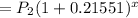
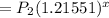
Thus, the ratio of the population of A and that of B is,

`\frac{\text{ Population of A}}{\text{Population of B}}=( P_1(1.05)^x)/( P_2(1.21551)^x)`

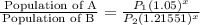
By equation (1),

`\frac{\text{ Population of A}}{\text{Population of B}}=( P_1(1.05)^x)/( P_1(1.21551)^x)`

`\frac{\text{ Population of A}}{\text{Population of B}}=( (1.05)^x)/( (1.21551)^x)`

`\frac{\text{ Population of A}}{\text{Population of B}}=((1.05)/(1.21551))^x`

`f(x)= (0.863834933)^x`

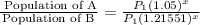
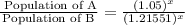
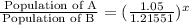
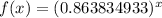
Which is the required function.