Question

An amusement park offers two options. Option 1 involves a $10 admission fee plus $0.50 per ride. Option 2 involves a $6 admission fee plus $0.75 per ride. For how many rides do the two options have the same cost ( or, what is the break-even point)?

Answer 1

16 rides

Explanation:

Option 1 . Admission fee = $10

Each ride = $0.50

Option 2 . Admission fee = $6

Each ride = $0.75

Let no. of rides be x

So, cost of ride according to option 1 = 0.50x

So, total cost after having x rides according to option 1 :

= 10+0.50x ---1

Cost of ride according to option 2 = 0.75x

So, total cost after having x rides according to option 2 :

= 6+0.75x --2

Now to find the beak even point i.e. having the same cost

Equate 1 and 2

`10+0.50x=6+ 0.75x`

`10-6= 0.75x-0.50x`

`4= 0.25x`

`(4)/(0.25) =x`

`16=x`

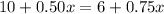
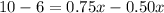
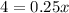
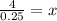
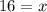
Thus for 16 rides , the two options have the same cost .

Hence the break even point is 16 rides