Answer:
Part A) Yes , the triangles are congruent
Part B) The side-angle-side (SAS) theorem
Part C) The perimeter of ∆PQR is
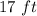
Explanation:
Step 1
we know that
The side-angle-side (SAS) theorem, states that: If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.
so in this problem
Traingle PQR and Triangle STU are congruent by the SAS Theorem
because
m<PQR=m<STU -------> included angle
PQ=TS
QR=TU
Step 2
Find the value of y
we know that
If the triangles are congruent
then
The corresponding sides are equal
so
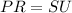
substitute
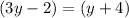
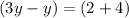

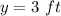
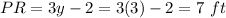
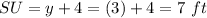
so
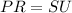
Step 3
Find the perimeter ∆PQR
Remember that
The perimeter of ∆PQR is equal to the perimeter ∆STU
The perimeter is equal to

substitute the values
