Question

The range of the function f(k) = k2 + 2k + 1 is {25, 64}. What is the function’s domain? A. {5, 8} B. {-5, -8} C. {3, 8} D. {4, 7} E. {4, 8}

Answer 1

Option D

The domain of the function is: {4, 7}

Explanation:

We know that for polynomial functions like
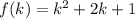`f(k) = k^2 + 2k + 1` its domain and its rank are all real numbers. However, for this case we are told that the function range is: the set {25, 64}

This means that the function is bounded.

Then the domain of f(k) are all possible values of k such that f(k) belongs to the interval {25, 64}.

To find the limit values of k then we do f(k) = 25

`k^2 + 2k + 1 = 25`

`k^2 + 2k -24 = 0`

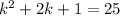
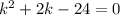
Now we factor the expression:

`(k + 6)(k-4) = 0`

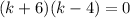
Then k = 4 and k = -6.

Now we do f(k) = 64

`k ^ 2 + 2k +1 = 64\\\\k ^ 2 + 2k -63 = 0`

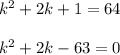
We factor the expression:

`(k + 9)(k-7) = 0`

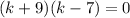
k = -9 and k = 7.

Finally we search between the options given an interval that matches.

The option that matches is option D {4, 7}

Finally, the domain of the function is: {4, 7}