Answer:
33 times
Explanation:
Total outcomes of rolling two cubes :
[1,1] ; [1,2] ; [1,3] ; [1,4] ; [1,5] ; [1,6]
[2,1] ; [2,2] ; [2,3] ; [2,4] ; [2,5] ; [2,6]
[3,1] ; [3,2] ; [3,3] ; [3,4] ; [3,5] ; [3,6]
[4,1] ; [4,2] ; [4,3] ; [4,4] ; [4,5] ; [4,6]
[5,1] ; [5,2] ; [5,3] ; [5,4] ; [5,5] ; [5,6]
[6,1] ; [6,2] ; [6,3] ; [6,4] ; [6,5] ; [6,6]
So, total no. of outcomes of rolling two cubes = 36
Favorable outcomes : roll a sum of 4 or less i.e. sum of 2,3,4
So, favorable outcomes :[1,1] ; [1,2] ; [2,1] ; [1,3] ; [3,1] ; [2,2] = 6
Thus the probability of getting a sum of 4 or less :
=
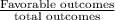
=
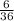
=

So, probability of getting sum of 4 or less is 1/6
Since he rolls each number cube 200 times
So, she expect to get a sum of 4 or less =
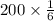 times
times
= 33.33
So, she would expect to roll a sum of 4 or less for 33 times .